Statistics is a mathematical body of science that pertains to the collection, analysis, interpretation or explanation, and presentation of data.
1.1.1 定义
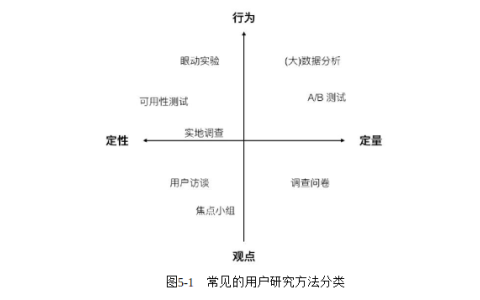
1.1.2 分类
1.2 统计数据有哪些?
1.2.1 不同的收集方法
1.2.2 不同的计量尺度
1.2.3 不同的时间状况
1.3 关于统计我们还需要知道些什么?
1.3.1 总体和样本
1.3.2 参数和统计量
1.3.3 变量
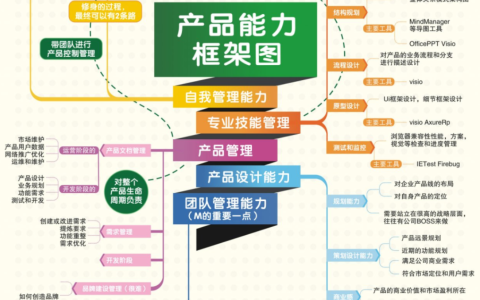
1.4 思维导图总结
参考资料:
[1] Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5. pp. 1–3
[2] 贾俊平等.,统计学(第七版)[M],北京,中国人民大学出版社,2018年1月
原创文章,作者:王得宇AIPM,如若转载,请注明出处:https://www.pmtemple.com/silence/10683/


 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫